Try the Free Math Solver or Scroll down to Resources!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Reducible and Irreducible Polynomials

Chapter 4: Reducible and Irreducible Polynomials
This worksheet reviews the facts about reducible and irreducible polynomials from Chapter 4.

Brute Force
Sometimes we can show a polynomial is irreducible simply by showing that none of the polynomials that could possibly be factors are factors.

1. Show that 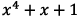is irreducible in 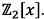Use an argument by contradiction. If 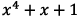is reducible, it has a factor of degree 1 or a factor of degree 2. Use long division or other arguments to show that none of these is actually a factor.

Checking All the Possible Roots
• If a polynomial with degree 2 or higher is irreducible in F(x), then it has no roots in F.
• If a polynomial with degree 2 or 3 has no roots in F, then it is irreducible in F(x).
Use these facts to answer the following questions.

2. Show that 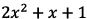is irreducible in 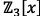by showing that it has no roots.

3. Consider the polynomial 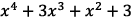in .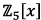
a. Show that this polynomial has no roots in .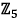
b. Can you conclude that the polynomial is irreducible?

Using Roots to Factor
Once we know a polynomial has a root x = a, we can factor x - a out of the polynomial using long division. Then we can try to factor the quotient.

4. Given that x = 3is a root of the polynomial 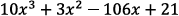in 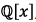factor the polynomial completely.

5. Consider the polynomial 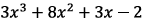in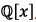
a. Use the Rational Root Theorem to make a list of all the possible rational roots of this polynomial.
b. Check each of the potential roots, and use your results to factor the polynomial completely.

6. Repeat problem 5, but with the polynomial .

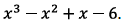Eisenstein’s Criterion
Eisenstein’s Criterion (Theorem 4.23 on page 111) is another method can be used to determine if a polynomial is irreducible. Note that if we can’t find a prime to make Eisenstein’s Criterion work, that does not tell us for certain that the polynomial is not irreducible.

7. Use Eisenstein’s Criterion to show that each of the following polynomials is irreducible in 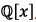Make sure to indicate which prime you are using.

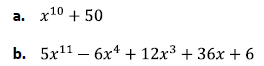
Reducing Mod p
The final method we have learned is reducing our polynomials mod a prime p. If we reduce the polynomial mod p and the result is reducible, then this doesn’t tell us anything.

8. Show that the following polynomials are irreduc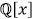ible in by finding a prime such that the polynomial is irreducible in .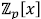

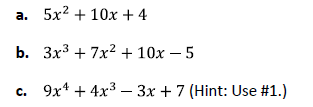
Selected Solutions
3b. No, the polynomial is reducible.

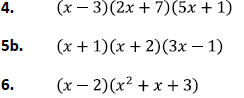
8c. In 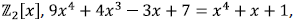which we showed is irreducible.