SOLVING EQUATIONS BY ADDING SUBTRACTION MULTIPLY DIVIDE
decimals to radical fractions chart
,
add subtract multiply divide integers worksheet
,
fractions to decimals convertion chart
,
lowest common denominator LCM codes
Thank you for visiting our site! You landed on this page because you entered a search term similar to this: solving equations by adding subtraction multiply divide.
We have an extensive database of resources on solving equations by adding subtraction multiply divide. Below is one of them. If you need further help, please take a look at our software "Algebrator", a software program that can solve any algebra problem you enter!
|
Steps for
Solving Equations
-
|
To perform these steps you will need to use a number of mathematical
properties of addition, subtraction, multiplication, and division.
The use of these properties, both in combining like terms and
isolating terms and variables, will be reviewed in this unit.
In the next unit we will solve equations containing two variables,
called multivariate equations.
Step 1: Combine Like Terms
As we learned in the last unit, like
terms are terms that contain
the same variable or group of variables raised to the same exponent,
regardless of their numerical coefficient.
Keeping in mind that an equation is a mathematical statement
that two expressions are equal, in this step
we will focus on combining like terms for the two expressions
contained in an equation. Since this unit deals only with equations
containing a single variable, there are not many like terms to
deal with. Let's look at an example. If we are given the equation
3z + 5 +2z = 12 + 3z, we need to first combine
like terms in each expression of this equation.
The two expressions in this equation are
3z + 5 +2z
and 12 + 4z. |
3z + 5 +2z = 12 + 4z |
|
There are three terms that contain the variable z: 3z,
2z, and 4z. We combine 3z, and 2z on
the left side of the equation, then subtract 4z from both
sides. |
(3z +2z) + 5 = 12 + 4z
5z + 5 – 4z = 12 + 4z – 4z
z + 5 = 12 |
Notice we chose to subtract 4z from both sides rather
than 5z. We chose to do this because consolidating in this
manner left z positive. However, subtracting 5z
from both sides would also be correct.
|
See how it works when we subtract 5z from both sides. |
5z + 5 – 5z = 12 + 4z – 5z
5 = 12 – z |
Step 2: Isolate the Terms that Contain the Variable
The main idea in solving equations is to isolate the variable
you want to solve for. This means we want to get terms containing
that variable on one side of the equation, with all other variables
and constants "moved" to the opposite side of the equation.
This section will address how we "move" terms from one
side of an equation to another, in order to isolate a variable,
using addition and its inverse property of subtraction.
The
Addition Property of Equality and
Its Inverse Property of Subtraction
If a = b, then a + c = b
+ c
If a = b, then a – d = b
– d
In other words, adding the same quantity to both sides of
an equation produces an equivalent equation.
Since subtraction is simply adding a negative number,
this rule applies when subtracting the same quantity from both
sides. |
Let's try this with the example: x + 3 = 15.
The key to solving this equation is to isolate x. On the left side of the equation,
x is added to 3. To undo this addition we must subtract
3 from both sides of the equation. It is important that we subtract
3 from both sides of the equation,
otherwise we will lose equality.
We now have:
|
Subtract 3 from both sides. |
(x + 3) – 3 = 15 – 3
x = 2 |
Here we solved for x by isolating it through
the use of inverse operations or in other words, by using opposite
operations. Addition and subtraction
are examples of inverses, and so are multiplication and division.
We can easily check the result we found above by substituting
12 for x in to the original equation\
|
The 12 works in this equation, so the answer is correct. |
12+ 3 = 15 |
The example we started in step one, 3z + 5 +2z
= 12 + 4z, is an example of an equation that contains more
than one term with a variable. In step one we combined all terms
containing the variable z. In this step we want to isolate
the variable z. To isolate z, choose one term containing
the variable z (usually the smaller one) to subtract from
both sides.
|
Subtract 5 from both sides to isolate the z. |
z + 5 – 5 = 12 – 5 |
|
This gives us our final result. |
z = 7 |
To be sure our answer is correct, we can check it by substituting
the solution back to the original equation, 3z + 5 +2z
= 12 + 4z:
|
The left side becomes: |
3 (7) + 5 + 2 (7)= 21 + 5 + 14 = 40 |
|
The right side becomes: |
12 + 4 (7) = 12 + 28 = 40 |
Notice that the right and left sides are equal, therefore we
have the correct solution. Now let’s look at some examples
of using addition and subtraction to solve equations.
Example
Solve the following equations for the variable in the
equation.
- 38 = z + 15
- 9x + 3 = 8x + 19
Answers
Solve the following equations for the variable in the
equation.
|
1. 38 = z + 15 |
23 = z
|
|
2. 9x + 3 = 8x + 19 |
x = 16
|
Detailed Answers
Solve the following equations for the variable in the
equation.
1. 38 = z + 15 23 = z
For this problem, we wish to isolate z on one
side of the equation.
|
Notice that in the original equation, 15 is added to z,
therefore we must perform the operation that is the inverse of
addition. This is subtraction. We must subtract 15 from both
sides of the equation. |
38 = z + 15
38 – 15 = z + 15 – 15
23 = z |
Again, to check your answer, replace the variable with the
solution in the original equation
|
The left side becomes: |
38 |
|
The right side becomes: |
(23) + 15 = 38 |
Both sides are equal, so our solution is correct.
2. 9x + 3 = 8x + 19 x = 16
In this equation we want to isolate the variable x
on one side of the equation. Note that x occurs on both
sides of the equation.
|
First apply the subtraction rule to the variables. We can subtract
8x from both sides. (You could have chosen to subtract
9x from both sides, but 8x was chosen because it’s
often useful to subtract the one with the smaller coefficient
since the result will be positive.) |
9x + 3 = 8x + 19
9x + 3 – 8x = 8x + 19 – 8x
9x – 8x + 3 = 8x – 8x
+ 19
x + 3 = 19 |
|
Once we isolate the x variable on one side of the equation,
we apply the subtraction property to the constants. |
x + 3 – 3 = 19 – 3
x = 16 |
Again, to check your answer, replace the variable with the
solution in the original equation.
|
The left side becomes: |
9 (16) + 3 = 144 + 3 = 147 |
|
The right side becomes: |
8 (16) + 19 = 128 + 19 = 147 |
Both sides are equal, so our solution is correct.
Step 3: Isolate The Variable You Wish To Solve For
In the examples in the previous section, by isolating the terms
containing the variable we wished to solve for, we were left with
a term that had a numerical coefficient of one, so the variable
was automatically isolated. However, if the variable does not
have a coefficient of one, we will need to isolate the variable
itself. When the variable we wish to isolate is either multiplied
or divided by a numerical coefficient or other variables that
are not equal to one, we need to use either multiplication or
division to isolate the variable.
The
Multiplication Property of Equality and
The Inverse Operation of Division
If a = b, then ac = bc
where c ¹ 0
If c = d, then c/e = d/e
where e ¹ 0
Multiplying both sides of an equation by the same nonzero
number produces an equivalent equation. We may adapt this property
to state that if we divide both sides of an equation by the same
nonzero number, we obtain an equivalent equation.
This fact follows from knowing that multiplying by the reciprocal
of a number is the same thing as dividing by that number.
c • 1/e is equivalent to c
÷ e
|
For example, suppose you want to solve the following equation
for x:
3x = 72
To solve this problem we want to isolate the x
variable. Since the numerical is multiplied by a numerical coefficient,
we can’t use addition or subtraction to do this.
|
Since x is multiplied by 3, we should use the inverse
operation of multiplication to isolate x. That means we
want to divide by 3. To isolate x, we simply divide both
sides of the equation by 3. |
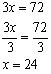
|
Again, what we do to one side of the equation, we must
also do to the other side of the equation. In this example we
divided both sides of the equation by 3.
Using the inverse operations procedure, work through the examples
below.
Example
Solve each of the equations for x.
- 6 = x/3
- (2/5) x = 8
Answers
Solve each of the equations for x.
|
1. 6 = x/3 |
18 = x |
|
2. (2/5) x = 8 |
x = 20 |
Detailed Answers
Solve each of the equations for x.
|
In this problem, the variable x is divided by 3.
To isolate x, you need to perform the inverse operation
of division, which is multiplication. This means we must multiply
both sides of the equation by 3. |
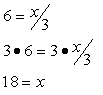 |
|
To check, replace the variable with the solution in the
original equation. |
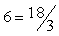 |
|
In this problem, the variable x is multiplied by 2 and
divided by 5. This means we must both divide the variable by
2 and multiply by 5 to isolate x. This is the same as
multiplying by the fraction 5/2. |
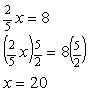 |
|
Again we should check our result by substituting the value we
got for x back into the equation. |
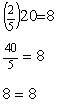 |
Step4: Substitute Your Answer into the Original Equation
Every answer should be checked to be sure it is correct. Substitution is a process of replacing
variables with numbers or expressions. By substituting,
we switch or exchange values, often replacing a variable with
a numerical value. We often substitute to minimize the number
of variables in an expression, or to actually evaluate the expression
or equation. For example, we are given the following:
a + 12 = b, and a =
9, find the value for b.
We can determine the value for the expression a + 12
by using substitution. Since we are given a = 9, we can
substitute 9 for a in the original expression:
9 + 12 = b
21 = b
After finding the solution for a variable, substitute the answer
into the original equation to be sure the equality holds true.
For example, in an earlier section we solved the following equation
for x:
3x = 72
We found the solution was x = 24. To check and be sure
this solution is correct we substitute 24 for x in the
original equation.
3x = 72 and x
= 24.
3(24) = 72
72 = 72
In each of the examples shown in this unit we have been doing
this step so you should be familiar with seeing this.
|
